Dim-DoE

Seit etwa 2011 arbeiten wir an dem Thema “Dim-DoE”, also Design of Experiments (DoE) für dimensionslose Kennzahlen (Dim). Über einfache Konzepte und Ideen hat Prof. Orth bei den DoE-Kongressen in Kassel in den Jahren 2012 und 2013 vorgetragen. Seine beiden Vorträge können Sie sich hier herunterladen: 2012: Dimensionsanalyse und Design of Experiments, 2013: Scale-Up eines Design Space vom Labor zur Produktion.

Im Frühjahr 2014 hat Prof. Orth die mathematischen Grundlagen zum Dim-DoE ausgearbeitet und mit zwei Beispielen untermauert. Das Paper ist für Nicht-Mathematiker schwer lesbar, aber vielleicht für den ein oder anderen mathematik-interssierten Ingenieur oder ingenieurnahen Statistiker oder Mathematiker interessant. Es kann hier abgerufen werden: 2020: The Dim-DoE framework for Scale-Up in Chemical Engineering. Die zugrunde liegenden R-Routinen wurden bisher noch nicht veröffentlicht, weil wir sie vorher noch verbessern möchten und noch mehr Anwendungserfahrung sammeln möchten.

Das Thema wurde 2013 auch in der Zeitschrift Technometrics, Volume 55, Issue 3, 2013, der American Statistical Society von Mark C. Albrecht, Christopher J. Nachtsheim, Thomas A. Albrecht & R. Dennis Cook aufgegriffen. Der Artikel ist verfügbar und kann von der Technometrics-Seite heruntergeladen werden: 2013: Experimental Design for Engineering Dimensional Analysis

Die Funktionsweise von Dim-DoE kann am besten am folgenden Bild veranschaulicht werden: Anstatt - beim zugegeben einfachen Prozess des Pendelschwungs - ein 3-Faktor Design für die dimensionsbehafteten Faktoren, Länge, Masse und Auslenkung zu machen, wird die dimensionslose Größe tan-alpha gebildet als Quotient Auslenkung/Länge und in dem Versuchsplan variiert. Das Design, ein 2^1-design mit einem Centre-point, im Bild die drei gelben Punkte, wird orthogonal (entlang der gelben Pfeile) zu der tan-alpha-Achse auf die gelbe durch die Gleichung, length = min, definierte Ebene projiziert und die Versuche werden durchgeführt.

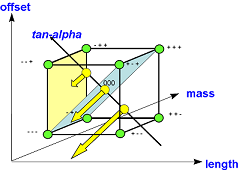
Die gemessene Zielgröße Periode ist nicht dimensionslos, aber die Zielgröße
t*sqrt(g/l) = Periode mal Wurzel(Erdbeschleunigung/Länge)
ist dimensionslos und somit ebenso wie der Faktor tan-alpha beim Scale-Up invariant. Sie wird abhängig von tan-alpha modelliert. Das Modell ist skalierbar!

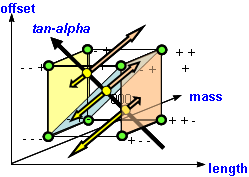
Modellprognosen für die dimensionslose Zielgröße, t*sqrt(g/l), können also orthogonal zur tan-alpha-Achse (entlang der orangen Pfeile) auf die Ebene, length = max, projiziert werden und auf die dimensionsbehaftete Zielgröße umgerechnet werden.

So gelang es Prof. Orth beim DoE-Kongress 2013 von einem 50 cm Marmeladeglaspendel auf ein fast 2m langes Bierflaschenpendel up-zu-scalen!